看了楼上大佬的解法,应该都没有想到 汉诺塔 与 二进制 还有一层微妙的关系,所以我来介绍一种 二进制解汉诺塔 的思路。
找规律
我们可以观察到这样一种规律:
二进制:需要前面全都变成 1 才能进位
汉诺塔:需要上面的盘子全都移走才能移动。
而这有相似之处。所以我们就可以想,可不可以用二进制来模拟圆盘的移动? 我们先来考虑一种简单的情况

来我们观察一下,假设汉诺塔的圆盘都在 A 柱上,我们从 0 数起(0000)

当我们把末位数从 0 变成 1 时,就把 0 号盘移动到右边的柱子上(如下图)

如果 0 已经在 C 柱上了

就把它移回 A 柱

要是在二进制计数中

已经进到了二位,也就是把末尾的两位数从 01 变成 10 的话

就移动 1 号圆盘

然而显然不能把它移到 B 柱上,所以就剩下 C 柱可以

当数到 11,只需要个位加一,所以只需移动 0 号圆盘
然后二进制中进到四位,所以移动 2 号圆盘

接下来以此类推:
个位加一,移动 0 盘;
二位加一,移动 1 盘;
三位加一,移动 2 盘;
...
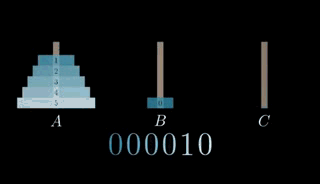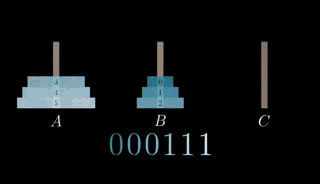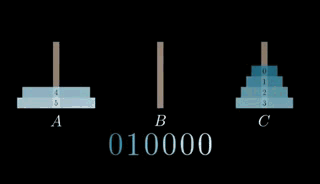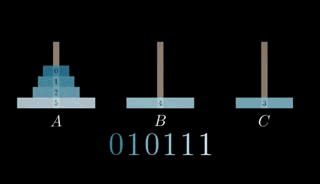
动画演示就像这样
证明
我们来证明一下这种思路的可行性。
汉诺塔的最少移动数的方案可以看作是要先把A柱上,最底面的圆盘以上的塔先移开,倒数第二盘要移动就要先把以上的圆盘移开,也就是一个递推的过程,而二进制的进位就是一个最简的递推方案。所以我们完全可以用二进制来模拟圆盘的移动。
关于此题
我们会发现,其实每一种汉诺塔的排列都会对应一个二进制数,二进制数转换成十进制数就是从 0000 推到现在这种排列的最少步数,那么这道题我们就可以先把给定初始状态的 A、B、C柱上的圆盘转换成二进制数,然后模拟二进制数一直加 1 的过程,得到目标状态。我们就可以很简单的解决这道题了。
提醒
A、B、C 三柱其实可以认为是不固定的,所以完全可以将初始状态的 A、B、C 柱上的圆盘进行交换以获取一个二进制数。
更新
2019/10/21 题解已发布,但是排版甚是难看,返工。

